–Ң‘и‚P‚P
Ѓ@‚Q‚В‚М•Ң•ыђ”‚МЉФ‚Й‚P‚В‚М”д—б’†ҚЂ‚Ғ‚ ‚иЃA•Ң•ыђ”‚Н•Ң•ыђ”‚Й‘О‚µ‚ДЃA•У‚Ғ•У‚Й‘О‚·‚й”д‚М‚QЏж‚М”д‚р‚а‚ВЃB

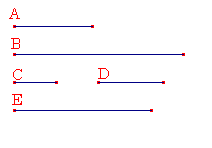
Ѓ@A‚ЖB‚р•Ң•ыђ”‚Ж‚µЃAC‚рA‚М•УЃAD‚рB‚М•У‚Ж‚№‚жЃB
Ѓ@A‚ЖB‚МЉФ‚Й‚P‚В‚М”д—б’†ҚЂ‚Ғ‚ ‚иЃAA‚НB‚Й‘О‚µЃAC‚ҒD‚Й‘О‚·‚й”д‚М‚QЏж‚М”д‚р‚а‚В‚ЖҺе’Ә‚·‚йЃB
Ѓ@C‚ЙD‚р‚©‚Ү‚ДE‚рҚм‚й‚Ж‚·‚йЃB
Ѓ@ҚҰЃAA‚Н•Ң•ыђ”‚ЕC‚Н‚»‚М•У‚И‚М‚ЕЃA‚»‚к‚䂦‚ЙЃAC‚Н‚»‚кҺ©ђg‚р‚©‚Ү‚ДA‚рҚм‚йЃB
Ѓ@“Ү‚¶—қ—R‚ЕЃAD‚Н‚»‚кҺ©ђg‚р‚©‚Ү‚ДB‚рҚм‚йЃB
Ѓ@‚»‚М‚Ж‚«ЃAC‚НCЃAD‚р‚©‚Ү‚ДЃA‚»‚к‚ә‚кA‚ЖE‚рҚм‚й‚М‚ЕЃA‚»‚к‚䂦‚ЙЃAC‚НD‚Й‘О‚µ‚ДЃAA‚НE‚Й‘О‚·‚йЃBproposition‡Z‚P‚V
Ѓ@“Ү‚¶—қ—R‚ЕЃAC‚НD‚Й‘О‚µ‚ДЃAE‚НB‚Й‘О‚·‚йЃB
Ѓ@‚»‚к‚䂦‚ЙЃAA‚НE‚Й‘О‚µ‚ДЃAE‚НB‚Й‘О‚·‚йЃBproposition‡Z‚P‚W
Ѓ@‚»‚к‚䂦‚ЙЃAA‚ЖB‚МЉФ‚Й‚P‚В‚М”д—б’†ҚЂ‚Ғ‚ ‚йЃB
Ѓ@Һџ‚ЙЃAA‚а‚Ь‚ҢB‚Й‘О‚µ‚ДЃAC‚ҒD‚Й‘О‚µ‚Д‚а‚В”д‚М‚QЏж‚М”д‚р‚а‚В‚ЖҺе’Ә‚·‚йЃB
Ѓ@AЃAEЃAB‚Н”д—б‚·‚й‚R‚В‚Мђ”‚И‚М‚ЕЃA‚»‚к‚䂦‚ЙЃAA‚НB‚Й‘О‚µ‚ДЃAA‚ҒE‚Й‘О‚µ‚Д‚а‚В”д‚М‚QЏж‚М”д‚р‚а‚ВЃBdefinition‡X‚X
Ѓ@‚µ‚©‚µЃAA‚НE‚Й‘О‚µ‚ДЃAC‚НD‚Й‘О‚·‚йЃB
Ѓ@‚»‚к‚䂦‚ЙЃAA‚НB‚Й‘О‚µ‚ДЃAC‚НD‚Й‘О‚µ‚Д‚а‚В”д‚М‚QЏж‚М”д‚р‚а‚ВЃB
Ѓ@‚»‚к‚䂦‚ЙЃA‚Q‚В‚М•Ң•ыђ”‚МЉФ‚Й‚P‚В‚М”д—б’†ҚЂ‚Ғ‚ ‚иЃA•Ң•ыђ”‚Н•Ң•ыђ”‚Й‘О‚µ‚ДЃA•У‚Ғ•У‚Й‘О‚·‚й”д‚М‚QЏж‚М”д‚р‚а‚ВЃB
ЏШ–ңЏI—№